堆
概念
堆是任意节点值满足大于等于(大根堆)或小于等于(小根堆)左右子节点值的完全二叉树
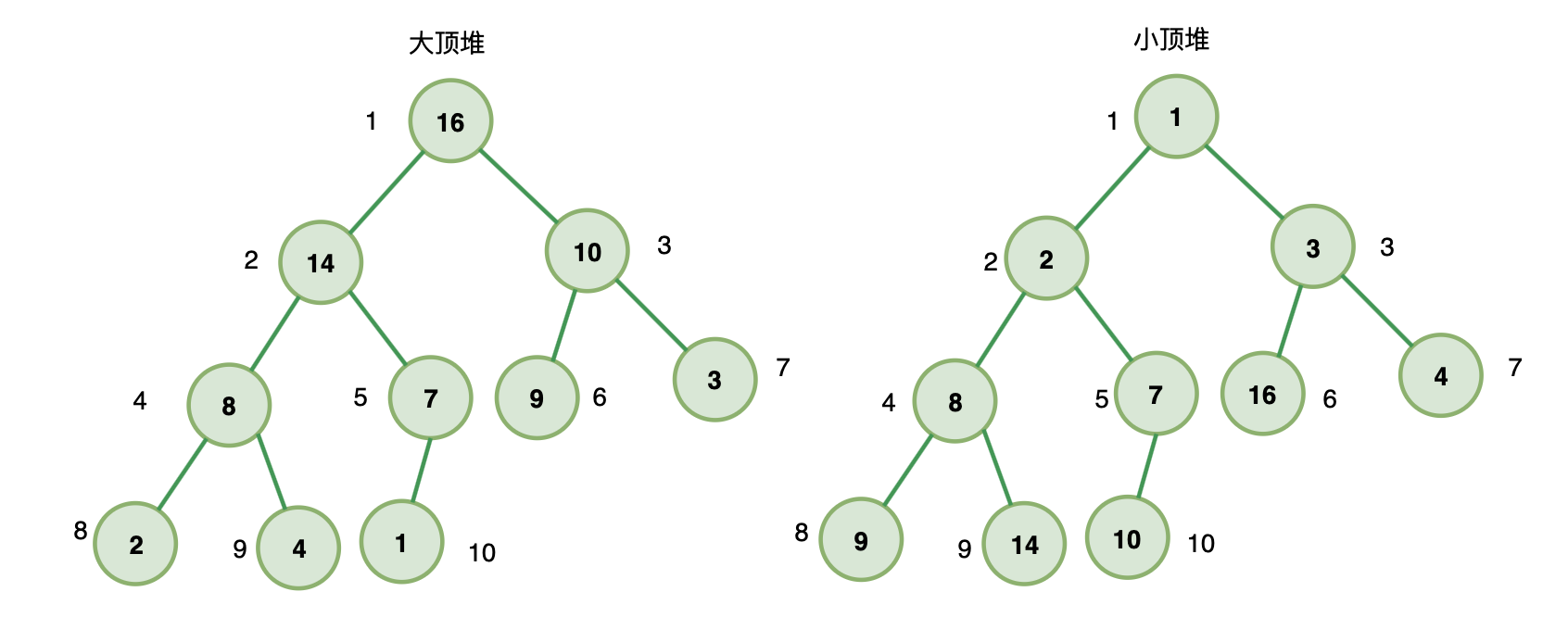
创建堆
堆的数组表示:可以用序号 1 ~ k 表示 k 个节点,如有一个节点序号为 k,那么父节点必定是 k/2 (取整),左子节点和右子节点分别为 2k 和 2k + 1 (也可以从 0 ~ k - 1 表示 k 个节点)
堆的操作方式:
插入(上移):从下往上,节点插入堆尾,然后调整:比父节点大就交换位置(大根堆),重复调整直到不需要调整或者到根节点
弹出(下移):从上往下,取出堆顶,最后一个节点移动到堆顶,然后从上往下调整堆,直到不需要调整或者到根节点
创建堆的方式有:
- 插入式创建
- 从前往后,从下往上:新建新的堆数组,对于需要排序的堆数组从前往后遍历节点,每一次把新的节点插入新的堆数组堆尾,然后调整:比父节点大就交换位置(大根堆),重复调整直到不需要调整或者到根节点
- 原地创建(堆化)
- 从前往后,从下往上:对于堆数组从前往后遍历节点,每一次跟上层的父节点进行对比,然后调整:比父节点大就交换位置(大根堆),重复调整直到不需要调整或者到根节点
- 从后往前,从上往下:对于堆数组从后往前遍历非叶子节点,每一次对比左右节点,然后调整:有一方比父节点大就交换位置(大根堆),重复调整直到不需要调整或到末尾节点
这两种创建方式的区别在于:一个是在新数组上创建堆,一个是在原来数组创建堆
参考:
前缀树
Trie,又称前缀树或字典树,是一棵有根树,其每个节点包含以下字段:
- 指向子节点的指针数组 children。
- 布尔字段 isEnd,表示该节点是否为字符串的结尾。
要点:
- 如果是哈希数组表示,children = [ ] 中,index 包含了字母的 ASCII 码信息,和一般的树节点有 val 不一样
- 叶子节点指向空节点,和一般树叶子节点值向 null 不一样
参考:
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1249118795@qq.com